Bernoulli’s principle describes how a fluid behaves while it moves. It creates a connection between a fluid flow’s height, velocity, and pressure. The Swiss mathematician and physicist Daniel Bernoulli developed the principle in 1738, and it bears his name. It is extensively utilised in a number of disciplines, such as engineering, aviation, and medicine.
Bernoulli’s Principle
According to Bernoulli’s principle, the total mechanical energy of an incompressible, non-viscous fluid moving in a streamlined fashion stays constant. This energy consists of:
Kinetic Energy (KE) – The energy due to the fluid’s motion.
Potential Energy (PE) – The energy due to the fluid’s height.
Pressure Energy (PE) – The energy due to the fluid’s pressure.
Mathematically, Bernoulli’s equation is written as:
P + 1 / 2 ρv2 + ρgh = constant
Where:
P = Pressure energy per unit volume (N/m²)
ρ = Density of the fluid (kg/m³)
v = Velocity of the fluid (m/s)
g = Acceleration due to gravity (9.8 m/s²)
h = Height of the fluid (m)
This equation means that if the speed of a fluid increases, its pressure decreases and vice versa.
Derivation of Bernoulli’s Equation
We apply the work-energy theorem to a small fluid element traveling down a streamline in order to obtain Bernoulli’s equation.
1. Think an incompressible fluid flowing steadily through a horizontal conduit.
2. The fluid element undergoes for the following work as a result of pressure forces at two points:
W = P1A1dx1 − P2A2dx2
The change in kinetic energy and potential energy is considered.
Using the conservation of energy principle, we obtain:
P1 + 1 / 2 ρv12 + ρgh1 = P2 + 1 / 2 ρv22 + ρgh2
This final equation represents Bernoulli’s theorem.
Applications of Bernoulli’s Principle
There are following uses of Bernoulli’s principle:
Aerodynamics (Aircraft Lift)
The airfoil, or wing, of an airplane is shaped to allow air to flow over the upper surface more quickly than the lower.
Bernoulli’s principle causes the top pressure to drop, generating lift that keeps the aircraft in the air.

Venturi Meter (Measuring Fluid Flow Rate)
A Venturi meter is a device that narrows a pipe, increasing velocity and decreasing pressure, to measure the velocity of a flowing fluid.
The flow rate is computed using the pressure differential.

Carburetor in Automobiles
A carburetor is used in internal combustion engines to mix fuel and air.
Air velocity rises as a result of the small route, forming a low-pressure area that facilitates fuel intake.
Spray Guns and Perfume Atomisers
o The pressure above a liquid drops when air is pushed over it.
o The liquid rises as a result, spraying as tiny droplets.
Blood Flow in Arteries (Medical Applications)
o Bernoulli’s principle governs how blood flows via arteries.
o Blood circulation is impacted by narrowed arteries since they have higher velocity and lower pressure.
Limitations of Bernoulli’s Principle
Despite its benefits, Bernoulli’s principle has many drawbacks.
1. It is only applicable to ideal fluids, which are non-viscous and incompressible.
2. It makes the assumption that the flow is constant and efficient, which isn’t always feasible in practical situations.
3. It ignores energy losses in fluids brought on by turbulence or friction.
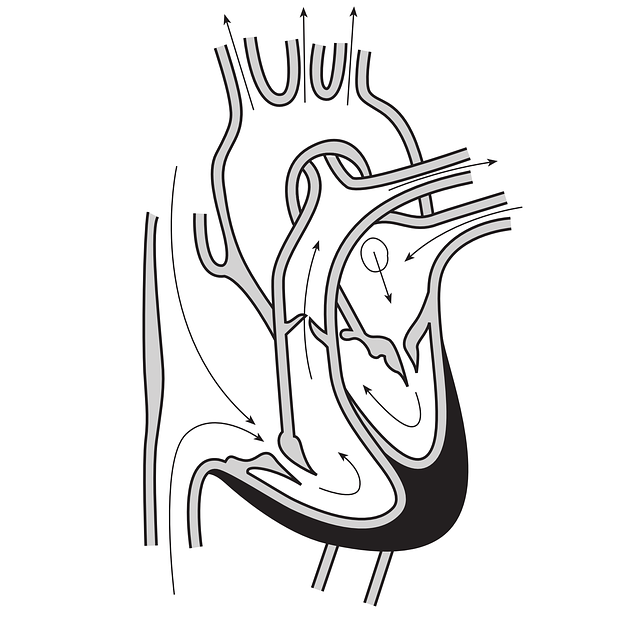
Blood flow and heart attack:
A persons suffering with advanced heart condition, the artery gets constricted to accumulation of plaque on its inner walls. In order to drive the blood through this constriction, a greater demand is placed on the activity of the heart. The speed of blood flow increases in this region.
From Bernoulli’s principle, the inside pressure drops and the artery may collapse due to external pressure. The exerts the further pressure to open the artery and forces the blood through. As the blood rushes through the opening, the internal pressure once again drops leading to repeat collapse. This phenomenon is called vascular flutter which can be heard on a stethoscope. This may result in a heart attack.
Dynamic lift of ball due to Magnus effect:
When a spinning ball is thrown, it deviates from its usual path in air. Due to difference in velocities of air, a pressure difference arises in lower and upper faces and the ball lifts upward by a net upward force. This dynamic lift due to spinning is called magnus effect.
Summary
Bernoulli’s principle explains how pressure, velocity, and height interact in fluid flow. It is essential for engineering, medicine, aviation, and everyday uses like blood flow and sprays. It is still one of the most effective resources for understanding the physics of moving fluids in spite of its drawbacks.
According to Bernoulli’s principle, the total of an incompressible, non-viscous fluid’s kinetic, potential, and pressure energies per unit volume stays constant when the fluid is flowing steadily. It clarifies how fluid velocity and pressure are related.
The Bernoulli equation is given by:
P + 1 / 2 ρv2 + ρgh = constant Where:
P = Pressure energy per unit volume
ρ = Density of fluid
v = Velocity of fluid
g = Acceleration due to gravity
h = Height above a reference point
Bernoulli’s principle is based on the following assumptions:
The fluid is incompressible.
The fluid flow is steady and streamlined.
The fluid has negligible viscosity (frictionless flow).
There is no external work or heat transfer involved.
Air flows over the upper surface of an airplane wing (airfoil) more quickly than it does over the bottom. Bernoulli’s principle states that higher pressure is created by slower-moving air below and lower pressure is created by faster-moving air above. The airplane can stay in the air because of the upward lift force created by this pressure differential.
Some practical applications include:
Aerodynamics (airplane lift, race car spoilers)
Venturi meter (fluid flow measurement)
Carburetors in engines (fuel mixing)
Perfume sprays and atomisers (low-pressure suction)
Blood flow in arteries (circulatory system effects)