Circular motion is describes the motion of an object along a circular path. This type of motion is common in both natural phenomena and human-made systems, ranging from the orbit of planets to the movement of vehicles on curved roads. Circular motion explains in more advanced such as rotational dynamics and planetary motion.
What is Circular Motion?
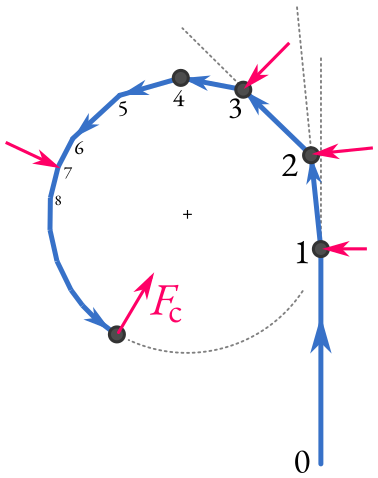
Circular motion occurs when an object moves along a circular path with a fixed radius. Unlike linear motion, where the path is straight, circular motion is constant change in the direction of the object’s velocity, even if the speed remains constant. This continuous change in direction means that the object experiences acceleration, even in uniform circular motion.
Types of Circular Motion
1.Uniform Circular Motion (UCM): In uniform circular motion, the object moves with constant speed along the circular path. However, even though the speed is constant, the velocity is not because the direction of motion keeps changing.
2. Non-uniform Circular Motion: In this type, the object’s speed varies as it moves along the circular path. This variation adds a tangential acceleration component in addition to the radial or centripetal acceleration.

Key Terms in Circular Motion
1.Radius (r): The distance from the center of the circle to the path of motion.
2. Angular Displacement (θ): The angle subtended by the object at the center of the circle during its motion.
3. Angular Velocity (ω): The rate at which the object sweeps out an angle at the center of the circle, measured in radians per second. ω = θ / t
4. Centripetal Force: A force directed toward the center of the circle that keeps the object in circular motion. It is given by:
Fc = mv2 / r
where m is the mass of the object, v is its velocity, and r is the radius of the circle.
5. Centripetal Acceleration (ac): The acceleration directed toward the center of the circle, keeping the object in circular motion.
ac = v2 / r
Dynamics of Circular Motion
Circular motion arises from a balance of forces. For example:
In planetary orbits: Gravitational force acts as the centripetal force.
In a car taking a curve: Friction between the tires and the road provides the necessary centripetal force.
If the required centripetal force is not sufficient, the object will deviate from the circular path, moving tangentially.
Applications of Circular Motion
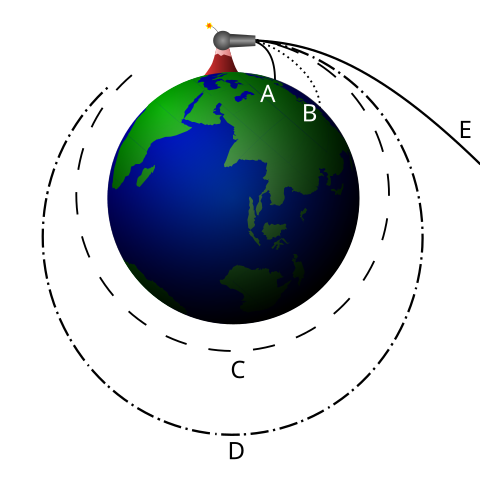
1.Astronomy and Space Science: The motion of planets around the Sun and satellites around the Earth are examples of circular motion governed by gravitational forces.
2. Transportation: Vehicles settle down with curved roads using the principles of circular motion. Banking of roads ensures safety by providing necessary centripetal force.
3. Daily Life Examples:
Spinning fans
Rotating wheels
Merry-go-rounds
4. Engineering:Circular motion principles are applied in designing roller coasters, gears, and turbines.
Real-Life Challenges in Circular Motion
1.Skidding on Curves: Insufficient friction on a curved path can lead to skidding. This is tackle by increasing the frictional force or banking the road.
2. Centrifugal Force Misinterpretation: Often mistaken as a real force, centrifugal force is the apparent force experienced in a rotating frame of reference, pushing an object outward. It is a pseudo-force due to inertia.
Fun Facts About Circular Motion
The Moon’s orbit around Earth and Earth’s orbit around the Sun are examples of nearly circular motion.
In roller coasters, circular loops create thrilling experiences by balancing centripetal force and gravity.
Important
Bending of cyclist on circular turning for safe going;
Component of normal reaction N sinθ provides centripetal force.
N sinθ = mv2 / r
N cosθ = mg
Maximum speed of cyclist, v2 = rg tanθ
Note
Circular motion is not only explains numerous natural phenomena but also has wide-ranging applications in engineering and daily life. Its principles help us to make sense of the forces at play in rotating systems, enhancing our ability to innovate and solve real problems. Whether it’s the complex movement of a planet’s orbit or the adventure of a roller coaster ride.
Circular motion is the motion of an object along a circular path. It can be classified into uniform circular motion, where the speed remains constant and non-uniform circular motion, where the speed varies.
Angular velocity (ω): It measures the rate of change of angular displacement, expressed in radians per second. ω = θ / t
Linear velocity (v): It is the tangential speed of the object moving in the circular path and is related to angular velocity by: v = r ⋅ ω
where r is the radius of the circle.
Centripetal force is the force that acts toward the center of the circular path, keeping the object in circular motion. Without this force, the object would move tangentially due to inertia. Its magnitude is given by: Fc = mv2 / r
where m is the mass, v is the velocity, and r is the radius of the circle.
Friction often acts as the source of centripetal force in situation like vehicles turning on curved roads. It prevents skidding by providing the necessary inward force to keep the object in circular motion.
Centripetal Force: A real force directed toward the center of the circular path, keeping the object in motion.
Centrifugal Force: A pseudo-force experienced in a rotating edge of location, which appears to push the object outward due to inertia.
In circular motion, the direction of velocity continuously changes. Since acceleration is the rate of change of velocity (both magnitude and direction), the object experiences centripetal acceleration toward the center of the circle. Its magnitude is: ac = v2 / r
Examples of circular motion are tabulated below:
The orbit of planets and satellites.
A car turning on a curved road.
The motion of a ceiling fan.
Spinning of a merry-go-round.
Wheels of a moving vehicle.