Kinematic equations describe the motion of objects under uniform (constant) acceleration, relating their displacement, velocity, acceleration, and time. These equations are foundational in understanding the motion of bodies under various forces. Uniform acceleration implies that velocity of an object changes at a constant rate throughout its motion, and these equations help to calculate key variables without needing detailed velocity-time data.
Here are the four main kinematic equations for uniformly accelerated motion:
v = u + at
s = ut + 1 / 2 at2
v2 = u2 + 2 as
s = u + v / 2 × t
where:
v = final velocity,
u = initial velocity,
a = acceleration,
t = time, and
s = displacement.
These equations can be derived from the basic definition of acceleration and are applied in uniformly accelerated motion, such as free-falling objects under gravity.
Detailed Explanation and Derivation of Equations :-
Equation 1: v = u + at
This equation shows how the final velocity v of an object is related to its initial velocity u, the constant acceleration a, and the time t of travel. Acceleration is defined as the rate of change of velocity:
a = v – u / t
Rearranging gives:
v = u + at
This equation helps us find the final velocity when initial velocity, acceleration, and time are known.
Equation 2: 1
s = ut + —– at2
2
The second equation describes the displacement s of an object. Using the concept of average velocity in uniformly accelerated motion, we find that displacement is given by:
s = average velocity × t
Since velocity changes linearly, the average velocity is the mean of the initial and final velocities, i.e. u + v
——-
2
Substituting from the first equation, we get
u + at
s = u + ——— x t
2
which simplifies to:
: 1
s = ut + —— at2
2
This equation is useful in finding the displacement when the initial velocity, acceleration, and time are known.
Equation 3: v2 = u2 + 2as
The third equation relates velocity and displacement, eliminating the time variable. By substituting
v − u
t = ——-
a
(from the first equation) into the second equation, we get:
v- u 1 v- u 2
s = u ——– + —- a ——–
a 2 a
Simplifying, we obtain:
v2 = u2 + 2as
This equation helps in cases where time is unknown but displacement, acceleration, and initial velocity are given.
Equation 4: u + v
s = ——- x t
2
The fourth equation is derived from the definition of average velocity. It calculates displacement s based on initial and final velocities without using acceleration. As the average velocity is
u + v the displacement can be found as:
——-
2
u + v
s = ——- x t
2
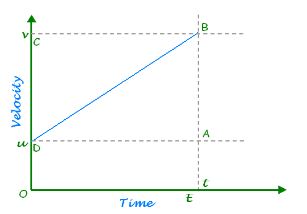
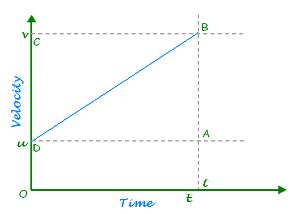
Graphical Representation of Kinematic Equations
The relationships in uniformly accelerated motion can be effectively visualised using graphs, particularly the velocity-time (v-t) graph and the displacement-time (s-t) graph.
In a velocity-time graph for uniformly accelerated motion, the slope represents acceleration. Since acceleration is constant, the graph is a straight line. The area under this line between t = 0 and t = t gives the displacement s. This is because:
Displacement = Area under the v-t graph =
1
——- (u + v) x t
2
Displacement-Time Graph
In the displacement-time graph, for uniformly accelerated motion, the curve is a parabola. Displacement increases quadratically with time, and the slope of this graph at any point gives the instantaneous velocity.
The parabolic shape reflects that the object’s velocity increases over time due to constant acceleration.
Application of Kinematic Equations :-
1. Free-Fall Motion: Objects under gravity fall with uniform acceleration, denoted g (approximately 9.8 m/s2 on Earth). By setting a = g and u = 0, we can find the velocity or displacement of a free-falling object at any point in time.
2. Projectile Motion: The vertical and horizontal motions of projectiles can be analyzed using these equations. The vertical component follows uniformly accelerated motion, governed by these equations, while the horizontal motion has a constant velocity
These kinematic equations are essential tools in physics for analyzing various motions under constant acceleration.
The kinematic equations for uniformly accelerated motion are four equations that describe the relationship between displacement, initial velocity, final velocity, acceleration, and time for an object moving with constant acceleration:
v = u + at
s = ut + 1 / 2at2
v2 = u2 + 2as
s = u + v / 2 × t
In these equations:
v is the final velocity,
u is the initial velocity,
a is the acceleration,
t is the time, and
s is the displacement.
These equations are applicable only when the object is moving with constant (uniform) acceleration. They are not valid if the acceleration is variable or if the object is in non-linear motion.
Displacement s can be calculated using the equation
1
s = ut + —– at2
2
where u is the initial velocity, a is the acceleration, and t is the time of travel.