Energy is a basic things that how objects move and interact. Potential energy, or the energy held in an object because of its position, configuration, or state, is a significant type of energy. This stored energy is an important because, under certain conditions, it can accomplish the work.
What is Potential Energy?
The energy that an object possesses as a result of its arrangement in relation to other objects or its position in a force field is known as potential energy, or PE.
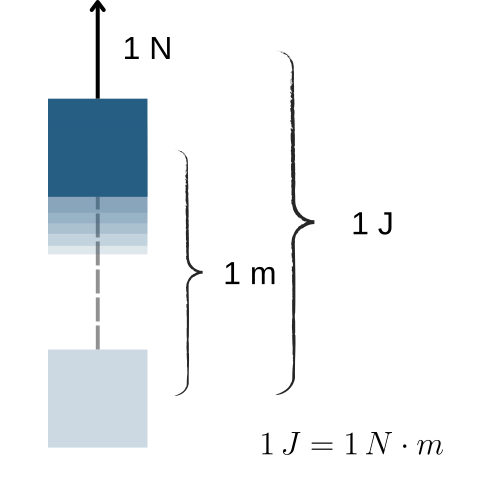
Potential energy is about the state or configuration of the thing, as opposed to kinetic energy, which is dependent on mobility. It is measured in joules (J) in the SI system and is a scalar quantity, which means it has only magnitude and no direction.
Types of Potential Energy
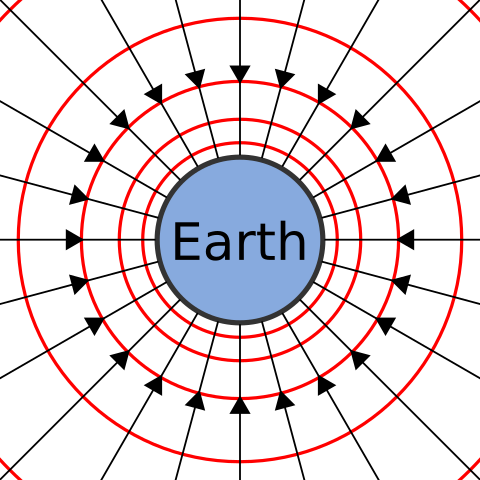
1.Gravitational Potential Energy (GPE): This is the energy that an object possesses as a result of its gravitational field position. An example of work against gravity is lifting a book off the ground; this labor is stored as gravitational potential energy.
The formula for GPE is: U = mgh
Here:
U is the gravitational potential energy,
m is the mass of the object,
g is the acceleration due to gravity (9.8 m/s2),
h is the height above the reference point.
2. Elastic Potential Energy: When an object, such as a rubber band or spring, is compressed or stretched, this kind of potential energy is created. When the object returns to its original shape, the energy that was stored in its deformation is released.
Elastic potential energy can be calculated as follows:
U = 1 / 2kx2
Here:
U is the elastic potential energy,
k is the spring constant (a measure of stiffness),
x is the displacement from the equilibrium position.
.
3. Electrostatic Potential Energy: This is the energy that the charged particle arrangement contains. For example, depending on their placements, two like charges repel one another while opposing charges attract, creating potential energy.

Key Characteristics of Potential Energy
• Position-Based: The relative positions of objects determine the potential energy. For example, an object’s gravitational potential energy increases with elevation.
Path-Independent: An object’s initial and ultimate positions, than the route used to get there, determine its potential energy.
• Stored Energy: This type of energy does not appear as motion but instead is kept in reserve and can be transformed into different forms is kinetic energy.
The Relationship Between Potential Energy and Work
The idea of work is closely related to potential energy. Energy is transmitted when an object undergoes work, and if this work causes the object’s position to change, the object’s potential energy also changes.
For example:
Lifting a ball increases its gravitational potential energy.
Compressing a spring stores elastic potential energy in it.
Work done (W) is equal to the change in potential energy (ΔU):
W = −ΔU The system’s potential energy is reduced by the work of conservative forces like gravity, as shown by the negative sign.
Conservative Forces and Potential Energy
Conservative forces those whose work is independent of the direction taken are the only ones for which potential energy is defined. Elastic and gravitational forces are two examples. Friction and other non-conservative forces release energy as heat or other forms, they do not store it in the same way.
Applications of Potential Energy
Potential energy is essential to many different occurrences and uses:
• Pendulums: A pendulum’s gravitational potential energy is greatest at the top of its swing.
• Roller Coasters: A coaster’s tremendous potential energy at the top of a hill is transformed into kinetic energy as it falls.
• Engineering and Architecture: Potential energy helps in designing stable structures and machines.
Note :-
How energy is stored and transformed in physical systems is deal with potential energy, such as the Earth’s gravitational pull and a spring’s stretch, are controlled by potential energy.
It is a basic component of physics because of its capacity to transform into kinetic energy and other forms, which enables us to examine and forecast how objects will behave in varied conditions. Potential energy is a concept which deals with mechanics, and energy conservation.
Kinetic energy is the energy a thing possesses as a result of motion, while potential energy is the energy held in an object as a result of its location, configuration, or condition. Like, potential energy is transformed into kinetic energy when a book falls from a height.
The main types of potential energy are:
Gravitational Potential Energy: It seen when an object, such as a stone, is raised above the ground.
Elastic potential energy: It is present in compressed or stretched materials, such as rubber bands or springs.
Electrostatic Potential Energy: Found in electric fields and between charged particles.