Relative velocity is an essential concept that helps us to understand motion from different reference points. In two dimensions, this concept becomes slightly more complex than in one dimension, as its components of motion are in both the x-axis and y-axis. This explain about projectile motion and fluid dynamics.
.
What is Relative Velocity?
Relative velocity is the velocity of one object as observed from another moving object. It gives the answers to the question: “How fast is one object moving relative to another?” This concept is particularly useful when analysing scenarios where two or more moving objects are there.
If two cars are moving in the same direction, their relative velocity would be the difference in their speeds. In two dimensions, we must consider both the magnitude and the direction of motion.
Motion of a particle with respect to an object which is also moving with respect to the ground then the velocity of particle w.r.t ground is its actual velocity (Vact) and velocity of particle w.r.t moving object is its relative velocity (Vrel) and the velocity of moving object (w.r.t ground) is the reference velocity (Vref).
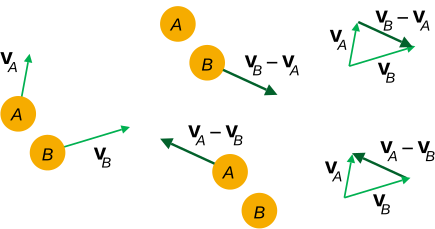
Relative Velocity in Two Dimensions
In two-dimensional motion, every object’s velocity can be expressed as a vector. A vector has two components:
1. Magnitude: The speed of the object.
2. Direction: The direction in which the object is moving.
To calculate the relative velocity, we subtract one velocity vector from another. Mathematically, if an object A has velocity vA and object B has velocity vB, the relative velocity of A with respect to B is:
vAB = vA−vB
Here, vAB represents how A moves relative to B.
Breaking It Down Into Components
In two dimensions, velocities are often broken into their x- and y-components:
x-component represents horizontal motion.
y-component represents vertical motion.
If vA = ( vAx, vAy ) and vB = ( vBx, vBy ), the relative velocity components are:
vABx = vAx−vBx
vABy = vAy−vByv
Resultant relative velocity vector is found using these components:
∣vAB∣2 = (vABx)2+ (vABy)2
The direction of the relative velocity is given by:
Θ = tan−1(vABy / vABx)
Example
Two boats in a river:
Boat A moves at 5 m/s north (positive y-direction).
Boat B moves at 3 m/s east (positive x-direction).
The relative velocity of boat A with respect to boat B is:
vAB = (0−3) I + (5−0) j = −3 I + 5 j
Magnitude:
∣vAB∣2 = (−3)2 + 52 = 9 + 25 = 34 m/s
Direction:
θ=tan−1 (5 / − 3)
This explain us the relative speed and direction of boat A as seen from boat B.
Key Points
1.Relative velocity depends on the frame of reference.
2. In two dimensions, it is vital to account for both x- and y-components of velocity.
3. Always use vector subtraction to find the relative velocity.
4. Use trigonometry to determine the direction of the resultant vector.
Applications of Relative Velocity
1.Collisions and search Problems: How objects approach or move away from each other.
2. Navigation: Determining the actual path of a moving vehicle or ship when affected by wind or water currents.
3.Projectile Motion: Calculating the motion of objects launched at an angle.
Few points to remember:
Swimming in the river:
A man can swim with velocity v i.e the velocity of man w.r.t still water. If water is also flowing with velocity VR then the velocity of man relative to ground
Vm = v + VR
If the swimming is in the direction of flow of water or along the downstream, then Vm = v + VR
If the swimming is in the direction opposite to the flow of water or along the upstream, then Vm = v – VR
If man swims across the river i.e v and vR are not collinear then use the vector algebra. Vm = v + VR
- Rain problem
In this section we will discuss at what angle should a man walking in rain, hold the umbrella so that he may not get wet. Here vRG , velocity of rain drops w.r.t ground, and VMG , velocity of man w.r.t ground vRG = ai + bj
Speed of rain w.r.t ground , (vRG )2 = a2 + b2
Angle (a) at which rain is falling with respect to ground tan α = a / b
VMG = vi Velocity of rain drops w.r.t manvRM = VRG + VMG
ai – bj – vi
(a – v) i -bj
Note
Relative velocity in two dimensions provides a powerful structure for analysing motion. By breaking velocities into components, applying vector subtraction, and using trigonometric principles, we can solve complex motion problems effectively.
Relative velocity in two dimensions is the velocity of one object as observed from another moving object, considering motion along both the x-axis and y-axis. It is represented as a vector and subtracting the velocity of the reference object from the observed object’s velocity.
To calculate relative velocity, subtract the velocity vector of one object (vB) from the other (vA): vAB = vA − vB
The x- and y-components are calculated separately:
vABx = vAx − vBx
vABy = vAy − vBy
Magnitude and direction can be derived from these components.
Breaking velocity into x- and y-components simplifies calculations by treating motion along each axis independently. This allows us to apply vector algebra to solve problems in a systematic way.
Relative velocity helps to analyse motion from different angle, making it easier to solve problems involving two or more moving objects, such as collisions, search scenarios, or navigation in moving fluids.
Yes, the relative velocity is zero when two objects move at the same speed and in the same direction. From each object’s perspective, the other appears stationary.
The direction of the relative velocity vector is given by the angle θ, calculated using:
θ=tan−1 vABy / vABx
This angle indicates the direction of motion relative to a chosen axis.
Relative velocity is applied in:
Analysing collisions and relative motion in physics problems.
Navigation, such as determining a boat’s actual velocity in a river with a current.
Aerodynamics, like understanding the effect of wind on an aircraft’s velocity.